Java Reading Set of Floating Point Values

IEEE Standard for floating-bespeak arithmetic

The IEEE Standard for Floating-Signal Arithmetics (IEEE 754) is a technical standard for floating-betoken arithmetic established in 1985 past the Institute of Electric and Electronics Engineers (IEEE). The standard addressed many problems found in the various floating-bespeak implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard.

The standard defines:

• arithmetic formats: sets of binary and decimal floating-point data, which consist of finite numbers (including signed zeros and subnormal numbers), infinities, and special "not a number" values (NaNs)
• interchange formats: encodings (chip strings) that may be used to substitution floating-point information in an efficient and compact form
• rounding rules: backdrop to be satisfied when rounding numbers during arithmetic and conversions
• operations: arithmetic and other operations (such as trigonometric functions) on arithmetics formats
• exception handling: indications of infrequent weather condition (such as segmentation by zero, overflow, etc.)

IEEE 754-2008, published in August 2008, includes near all of the original IEEE 754-1985 standard, plus the IEEE 854-1987 Standard for Radix-Contained Floating-Point Arithmetic. The electric current version, IEEE 754-2019, was published in July 2019.^[i] It is a pocket-sized revision of the previous version, incorporating mainly clarifications, defect fixes and new recommended operations.

Standard evolution [edit]

The offset standard for floating-point arithmetic, IEEE 754-1985, was published in 1985. It covered but binary floating-point arithmetic.

A new version, IEEE 754-2008, was published in August 2008, post-obit a 7-year revision procedure, chaired past Dan Zuras and edited past Mike Cowlishaw. Information technology replaced both IEEE 754-1985 (binary floating-point arithmetics) and IEEE 854-1987 Standard for Radix-Contained Floating-Point Arithmetics. The binary formats in the original standard are included in this new standard forth with three new basic formats, one binary and two decimal. To adjust to the current standard, an implementation must implement at to the lowest degree one of the basic formats every bit both an arithmetics format and an interchange format.

The international standard ISO/IEC/IEEE 60559:2011 (with content identical to IEEE 754-2008) has been canonical for adoption through JTC1/SC 25 nether the ISO/IEEE PSDO Agreement^{[2] [iii]} and published.^[iv]

The current version, IEEE 754-2019 published in July 2019, is derived from and replaces IEEE 754-2008, post-obit a revision procedure started in September 2015, chaired past David G. Hough and edited by Mike Cowlishaw. It incorporates mainly clarifications (east.chiliad. totalOrder) and defect fixes (e.grand. minNum), but also includes some new recommended operations (eastward.g. augmentedAddition).^{[5] [6]}

The international standard ISO/IEC 60559:2020 (with content identical to IEEE 754-2019) has been approved for adoption through JTC1/SC 25 and published.^[vii]

The side by side projected revision of the standard is in 2028.^[8]

Formats [edit]

An IEEE 754 format is a "set of representations of numerical values and symbols". A format may likewise include how the gear up is encoded.^[ix]

A floating-point format is specified by:

• a base (too called radix) b, which is either 2 (binary) or 10 (decimal) in IEEE 754;
• a precision p;
• an exponent range from emin to emax, with emin = 1 − emax for all IEEE 754 formats.

A format comprises:

• Finite numbers, which can be described by three integers: southward = a sign (zero or one), c = a significand (or coefficient) having no more than p digits when written in base b (i.e., an integer in the range through 0 to b ^p  − i), and q = an exponent such that emin ≤ q +p − 1 ≤ emax. The numerical value of such a finite number is (−one) ^s × c × b ^q .^[a] Moreover, there are two zero values, called signed zeros: the sign bit specifies whether a goose egg is +0 (positive zero) or −0 (negative zero).
• Two infinities: +∞ and −∞.
• Ii kinds of NaN (not-a-number): a placidity NaN (qNaN) and a signaling NaN (sNaN).

For instance, if b = 10, p = 7, and emax = 96, so emin = −95, the significand satisfies 0 ≤ c ≤ 9999 999 , and the exponent satisfies −101 ≤ q ≤ xc. Consequently, the smallest non-zero positive number that can be represented is 1×10⁻¹⁰¹, and the largest is 9999999×10⁹⁰ (ix.999999×10⁹⁶), and then the full range of numbers is −9.999999×10⁹⁶ through 9.999999×10⁹⁶. The numbers −b ^one−emax and b ^one−emax (here, −i×10⁻⁹⁵ and 1×ten⁻⁹⁵) are the smallest (in magnitude) normal numbers; non-aught numbers betwixt these smallest numbers are chosen subnormal numbers.

Representation and encoding in memory [edit]

Some numbers may have several possible exponential format representations. For example, if b = 10, and p = seven, then −12.345 can exist represented by −12345×10⁻ⁱⁱⁱ, −123450×10^−iv, and −1234500×10⁻⁵. However, for most operations, such as arithmetic operations, the effect (value) does not depend on the representation of the inputs.

For the decimal formats, whatever representation is valid, and the set up of these representations is called a cohort. When a issue can have several representations, the standard specifies which member of the cohort is chosen.

For the binary formats, the representation is fabricated unique by choosing the smallest representable exponent allowing the value to be represented exactly. Further, the exponent is non represented directly, but a bias is added so that the smallest representable exponent is represented as i, with 0 used for subnormal numbers. For numbers with an exponent in the normal range (the exponent field being neither all ones nor all zeros), the leading bit of the significand will always be 1. Consequently, a leading 1 can exist implied rather than explicitly present in the retention encoding, and under the standard the explicitly represented part of the significand will lie between 0 and i. This rule is called leading bit convention, implicit bit convention, or hidden bit convention. This rule allows the binary format to have an actress scrap of precision. The leading bit convention cannot exist used for the subnormal numbers every bit they accept an exponent outside the normal exponent range and scale by the smallest represented exponent every bit used for the smallest normal numbers.

Due to the possibility of multiple encodings (at least in formats called interchange formats), a NaN may comport other information: a sign scrap (which has no meaning, just may exist used past some operations) and a payload, which is intended for diagnostic information indicating the source of the NaN (but the payload may have other uses, such as NaN-boxing ^{[x] [11] [12]}).

Bones and interchange formats [edit]

The standard defines five basic formats that are named for their numeric base of operations and the number of bits used in their interchange encoding. In that location are three binary floating-signal bones formats (encoded with 32, 64 or 128 bits) and 2 decimal floating-point basic formats (encoded with 64 or 128 $.25). The binary32 and binary64 formats are the single and double formats of IEEE 754-1985 respectively. A conforming implementation must fully implement at to the lowest degree one of the basic formats.

The standard besides defines interchange formats, which generalize these basic formats.^[13] For the binary formats, the leading flake convention is required. The following table summarizes the smallest interchange formats (including the basic ones).

Proper name	Mutual name	Base	Significand bits[b] or digits	Decimal digits	Exponent $.25	Decimal E max	Exponent bias[14]	Eastward min	Eastward max	Notes
binary16	One-half precision	2	eleven	3.31	5	iv.51	iifour−1 = 15	−14	+fifteen	not bones
binary32	Single precision	2	24	7.22	8	38.23	27−1 = 127	−126	+127
binary64	Double precision	two	53	xv.95	11	307.95	210−1 = 1023	−1022	+1023
binary128	Quadruple precision	2	113	34.02	15	4931.77	ii14−1 = 16383	−16382	+16383
binary256	Octuple precision	ii	237	71.34	xix	78913.2	218−1 = 262143	−262142	+262143	non basic
decimal32		10	vii	7	7.58	96	101	−95	+96	not basic
decimal64		10	16	16	9.58	384	398	−383	+384
decimal128		10	34	34	xiii.58	6144	6176	−6143	+6144

Note that in the table higher up, the minimum exponents listed are for normal numbers; the special subnormal number representation allows fifty-fifty smaller numbers to be represented (with some loss of precision). For example, the smallest positive number that can exist represented in binary64 is 2⁻¹⁰⁷⁴; contributions to the −1074 figure include the East min value −1022 and all merely i of the 53 significand bits (2^{−1022 − (53 − ane)} = 2⁻¹⁰⁷⁴).

Decimal digits is digits × log₁₀ base of operations. This gives an approximate precision in number of decimal digits.

Decimal E max is Emax × log₁₀ base. This gives an judge value of the maximum decimal exponent.

The binary32 (single) and binary64 (double) formats are two of the most common formats used today. The figure below shows the absolute precision for both formats over a range of values. This effigy tin can be used to select an appropriate format given the expected value of a number and the required precision.

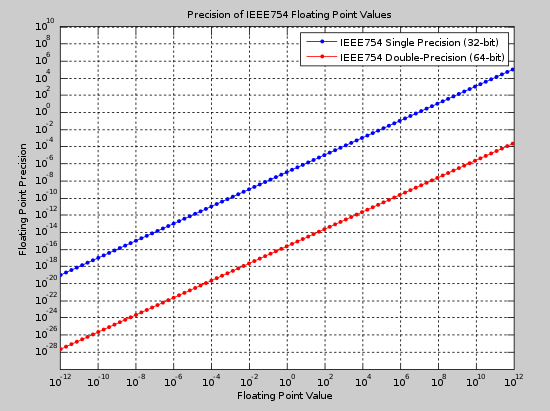
Precision of binary32 and binary64 in the range 10⁻¹² to ten¹²

An case of a layout for 32-bit floating point is

and the 64 scrap layout is like.

Extended and extendable precision formats [edit]

The standard specifies optional extended and extendable precision formats, which provide greater precision than the bones formats.^[xv] An extended precision format extends a basic format by using more precision and more than exponent range. An extendable precision format allows the user to specify the precision and exponent range. An implementation may utilize whatever internal representation information technology chooses for such formats; all that needs to exist defined are its parameters (b, p, and emax). These parameters uniquely describe the fix of finite numbers (combinations of sign, significand, and exponent for the given radix) that information technology can stand for.

The standard recommends that language standards provide a method of specifying p and emax for each supported base b.^[16] The standard recommends that language standards and implementations support an extended format which has a greater precision than the largest basic format supported for each radix b.^[17] For an extended format with a precision betwixt two basic formats the exponent range must be every bit bang-up equally that of the next wider basic format. And then for instance a 64-bit extended precision binary number must take an 'emax' of at to the lowest degree 16383. The x87 lxxx-fleck extended format meets this requirement.

Interchange formats [edit]

Interchange formats are intended for the commutation of floating-signal information using a chip string of fixed length for a given format.

Binary [edit]

For the exchange of binary floating-indicate numbers, interchange formats of length 16 bits, 32 bits, 64 bits, and whatsoever multiple of 32 bits ≥ 128^[c] are divers. The 16-bit format is intended for the substitution or storage of small numbers (e.g., for graphics).

The encoding scheme for these binary interchange formats is the aforementioned equally that of IEEE 754-1985: a sign bit, followed past west exponent $.25 that describe the exponent offset by a bias, and p − 1 bits that describe the significand. The width of the exponent field for a k-bit format is computed as w = round(four log_ii(one thousand)) − 13. The existing 64- and 128-bit formats follow this dominion, but the 16- and 32-scrap formats have more exponent $.25 (five and 8 respectively) than this formula would provide (three and 7 respectively).

As with IEEE 754-1985, the biased-exponent field is filled with all 1 $.25 to indicate either infinity (trailing significand field = 0) or a NaN (abaft significand field ≠ 0). For NaNs, quiet NaNs and signaling NaNs are distinguished by using the nearly meaning bit of the trailing significand field exclusively,^[d] and the payload is carried in the remaining bits.

Decimal [edit]

For the exchange of decimal floating-indicate numbers, interchange formats of any multiple of 32 bits are divers. As with binary interchange, the encoding scheme for the decimal interchange formats encodes the sign, exponent, and significand. 2 different bit-level encodings are divers, and interchange is complicated by the fact that some external indicator of the encoding in utilise may be required.

The ii options allow the significand to be encoded equally a compressed sequence of decimal digits using densely packed decimal or, alternatively, as a binary integer. The former is more convenient for directly hardware implementation of the standard, while the latter is more suited to software emulation on a binary calculator. In either case, the set of numbers (combinations of sign, significand, and exponent) that may be encoded is identical, and special values (±zilch with the minimum exponent, ±infinity, serenity NaNs, and signaling NaNs) have identical encodings.

Rounding rules [edit]

The standard defines five rounding rules. The first ii rules round to a nearest value; the others are called directed roundings:

Roundings to nearest [edit]

• Round to nearest, ties to even – rounds to the nearest value; if the number falls midway, it is rounded to the nearest value with an even least significant digit; this is the default for binary floating signal and the recommended default for decimal.
• Circular to nearest, ties abroad from null – rounds to the nearest value; if the number falls midway, it is rounded to the nearest value above (for positive numbers) or below (for negative numbers); this is intended as an selection for decimal floating point.

Directed roundings [edit]

• Round toward 0 – directed rounding towards aught (also known as truncation).
• Round toward +∞ – directed rounding towards positive infinity (also known equally rounding upwards or ceiling).
• Round toward −∞ – directed rounding towards negative infinity (also known every bit rounding down or flooring).

Example of rounding to integers using the IEEE 754 rules

Mode	Instance value
	+11.5	+12.5	−11.5	−12.5
to nearest, ties to even	+12.0	+12.0	−12.0	−12.0
to nearest, ties away from aught	+12.0	+13.0	−12.0	−13.0
toward 0	+eleven.0	+12.0	−11.0	−12.0
toward +∞	+12.0	+thirteen.0	−11.0	−12.0
toward −∞	+11.0	+12.0	−12.0	−13.0

Unless specified otherwise, the floating-point outcome of an operation is adamant by applying the rounding role on the infinitely precise (mathematical) consequence. Such an operation is said to exist correctly rounded. This requirement is called correct rounding.^[eighteen]

Required operations [edit]

Required operations for a supported arithmetic format (including the bones formats) include:

• Arithmetic operations (add, decrease, multiply, carve up, square root, fused multiply–add together, remainder)^{[19] [20]}
• Conversions (between formats, to and from strings, etc.)^{[21] [22]}
• Scaling and (for decimal) quantizing^{[23] [24]}
• Copying and manipulating the sign (abs, negate, etc.)^[25]
• Comparisons and total ordering^{[26] [27]}
• Classification and testing for NaNs, etc. ^[28]
• Testing and setting flags^[29]
• Miscellaneous operations.^{[ specify ]}

Comparison predicates [edit]

The standard provides comparison predicates to compare one floating-point datum to another in the supported arithmetics format.^[xxx] Any comparison with a NaN is treated as unordered. −0 and +0 compare every bit equal.

Total-ordering predicate [edit]

The standard provides a predicate totalOrder, which defines a total ordering on canonical members of the supported arithmetics format.^[31] The predicate agrees with the comparison predicates when 1 floating-point number is less than the other. The totalOrder predicate does not impose a total ordering on all encodings in a format. In particular, information technology does not distinguish amidst dissimilar encodings of the same floating-point representation, as when 1 or both encodings are not-canonical.^[32] IEEE 754-2019 incorporates clarifications of totalOrder.

For the binary interchange formats whose encoding follows the IEEE 754-2008 recommendation on placement of the NaN signaling fleck, the comparison is identical to i that type puns the floating-point numbers to a sign–magnitude integer (assuming a payload ordering consistent with this comparing), an old trick for FP comparison without an FPU.^[33]

Exception handling [edit]

The standard defines five exceptions, each of which returns a default value and has a corresponding status flag that is raised when the exception occurs.^[e] No other exception handling is required, only boosted not-default alternatives are recommended (see § Alternate exception handling).

The five possible exceptions are:

• Invalid operation: mathematically undefined, e.g., the foursquare root of a negative number. By default, returns qNaN.
• Sectionalisation by zip: an operation on finite operands gives an exact space outcome, e.g., 1/0 or log(0). By default, returns ±infinity.
• Overflow: a finite result is likewise big to be represented accurately (i.east., its exponent with an unbounded exponent range would be larger than emax). Past default, returns ±infinity for the round-to-nearest modes (and follows the rounding rules for the directed rounding modes).
• Underflow: a result is very small (outside the normal range). By default, returns a number less than or equal to the minimum positive normal number in magnitude (following the rounding rules); a subnormal always implies an underflow exception, but by default, if it is exact, no flag is raised.
• Inexact: the exact (i.east., unrounded) result is not representable exactly. By default, returns the correctly rounded issue.

These are the same five exceptions as were divers in IEEE 754-1985, but the partition by zero exception has been extended to operations other than the sectionalisation.

Some decimal floating-point implementations define additional exceptions,^{[34] [35]} which are not part of IEEE 754:

• Clamped: a result's exponent is also large for the destination format. Past default, abaft zeros will be added to the coefficient to reduce the exponent to the largest usable value. If this is non possible (considering this would cause the number of digits needed to be more than the destination format) then an overflow exception occurs.
• Rounded: a result's coefficient requires more than digits than the destination format provides. An inexact exception is signaled if any non-nothing digits are discarded.

Additionally, operations similar quantize when either operand is space, or when the result does not fit the destination format, will also signal invalid operation exception.^[36]

Recommendations [edit]

Alternate exception handling [edit]

The standard recommends optional exception treatment in various forms, including presubstitution of user-defined default values, and traps (exceptions that change the flow of control in some mode) and other exception handling models that interrupt the period, such as try/grab. The traps and other exception mechanisms remain optional, equally they were in IEEE 754-1985.

Recommended operations [edit]

Clause 9 in the standard recommends additional mathematical operations^[37] that language standards should define.^[38] None are required in order to conform to the standard.

Recommended arithmetic operations, which must round correctly:^[39]

• ${\displaystyle e^{x}}$ , ${\displaystyle 2^{ten}}$ , ${\displaystyle 10^{x}}$
• ${\displaystyle e^{x}-1}$ , ${\displaystyle 2^{x}-1}$ , ${\displaystyle 10^{x}-one}$
• ${\displaystyle \ln x}$ , ${\displaystyle \log _{ii}x}$ , ${\displaystyle \log _{ten}x}$
• ${\displaystyle \ln(1+x)}$ , ${\displaystyle \log _{ii}(1+x)}$ , ${\displaystyle \log _{10}(1+x)}$
• ${\displaystyle {\sqrt {x^{2}+y^{two}}}}$
• ${\displaystyle {\sqrt {ten}}}$
• ${\displaystyle (1+x)^{north}}$
• ${\displaystyle x^{\frac {1}{n}}}$
• ${\displaystyle x^{n}}$ , ${\displaystyle x^{y}}$
• ${\displaystyle \sin x}$ , ${\displaystyle \cos ten}$ , ${\displaystyle \tan ten}$
• ${\displaystyle \arcsin ten}$ , ${\displaystyle \arccos x}$ , ${\displaystyle \arctan 10}$ , ${\displaystyle \operatorname {atan2} (y,x)}$
• ${\displaystyle \operatorname {sinPi} x=\sin \pi x}$ , ${\displaystyle \operatorname {cosPi} x=\cos \pi 10}$ , ${\displaystyle \operatorname {tanPi} ten=\tan \pi 10}$ (meet also: Multiples of π)
• ${\displaystyle \operatorname {asinPi} 10={\frac {\arcsin 10}{\pi }}}$ , ${\displaystyle \operatorname {acosPi} ten={\frac {\arccos ten}{\pi }}}$ , ${\displaystyle \operatorname {atanPi} x={\frac {\arctan x}{\pi }}}$ , ${\displaystyle \operatorname {atan2Pi} (y,10)={\frac {\operatorname {atan2} (y,x)}{\pi }}}$ (come across besides: Multiples of π)
• ${\displaystyle \sinh x}$ , ${\displaystyle \cosh x}$ , ${\displaystyle \tanh x}$
• ${\displaystyle \operatorname {arsinh} x}$ , ${\displaystyle \operatorname {arcosh} x}$ , ${\displaystyle \operatorname {artanh} x}$

The asinPi, acosPi and tanPi functions were not part of the IEEE 754-2008 standard considering they were accounted less necessary.^[forty] asinPi, acosPi were mentioned, only this was regarded as an fault.^[five] All 3 were added in the 2019 revision.

The recommended operations also include setting and accessing dynamic fashion rounding direction,^[41] and implementation-divers vector reduction operations such as sum, scaled product, and dot product, whose accuracy is unspecified by the standard.^[42]

Equally of 2019^[update], augmented arithmetic operations ^[43] for the binary formats are also recommended. These operations, specified for addition, subtraction and multiplication, produce a pair of values consisting of a upshot correctly rounded to nearest in the format and the error term, which is representable exactly in the format. At the time of publication of the standard, no hardware implementations are known, but very like operations were already implemented in software using well-known algorithms. The history and motivation for their standardization are explained in a groundwork document.^{[44] [45]}

Equally of 2019, the formerly required minNum, maxNum, minNumMag, and maxNumMag in IEEE 754-2008 are now deleted due to their non-associativity. Instead, ii sets of new minimum and maximum operations are recommended.^[46] The commencement set contains minimum, minimumNumber, maximum and maximumNumber. The 2d set contains minimumMagnitude, minimumMagnitudeNumber, maximumMagnitude and maximumMagnitudeNumber. The history and motivation for this modify are explained in a background document.^[47]

Expression evaluation [edit]

The standard recommends how language standards should specify the semantics of sequences of operations, and points out the subtleties of literal meanings and optimizations that change the value of a event. Past contrast, the previous 1985 version of the standard left aspects of the language interface unspecified, which led to inconsistent behavior between compilers, or different optimization levels in an optimizing compiler.

Programming languages should allow a user to specify a minimum precision for intermediate calculations of expressions for each radix. This is referred to as preferredWidth in the standard, and it should be possible to set this on a per-cake basis. Intermediate calculations within expressions should be calculated, and whatever temporaries saved, using the maximum of the width of the operands and the preferred width if set. Thus, for instance, a compiler targeting x87 floating-signal hardware should accept a ways of specifying that intermediate calculations must employ the double-extended format. The stored value of a variable must e'er exist used when evaluating subsequent expressions, rather than any forerunner from earlier rounding and assigning to the variable.

Reproducibility [edit]

The IEEE 754-1985 version of the standard allowed many variations in implementations (such every bit the encoding of some values and the detection of certain exceptions). IEEE 754-2008 has reduced these allowances, only a few variations still remain (especially for binary formats). The reproducibility clause recommends that linguistic communication standards should provide a means to write reproducible programs (i.east., programs that will produce the same outcome in all implementations of a language) and describes what needs to be done to reach reproducible results.

Character representation [edit]

The standard requires operations to convert between bones formats and external character sequence formats.^[48] Conversions to and from a decimal character format are required for all formats. Conversion to an external character sequence must be such that conversion back using circular to nearest, ties to even will recover the original number. There is no requirement to preserve the payload of a quiet NaN or signaling NaN, and conversion from the external grapheme sequence may turn a signaling NaN into a quiet NaN.

The original binary value will be preserved past converting to decimal and back once more using:^[49]

• 5 decimal digits for binary16,
• ix decimal digits for binary32,
• 17 decimal digits for binary64,
• 36 decimal digits for binary128.

For other binary formats, the required number of decimal digits is^[f]

${\displaystyle 1+\lceil p\log _{10}(2)\rceil ,}$

where p is the number of significant bits in the binary format, e.g. 237 bits for binary256.

When using a decimal floating-betoken format, the decimal representation will exist preserved using:

• 7 decimal digits for decimal32,
• 16 decimal digits for decimal64,
• 34 decimal digits for decimal128.

Algorithms, with code, for correctly rounded conversion from binary to decimal and decimal to binary are discussed by Gay,^[50] and for testing – by Paxson and Kahan.^[51]

Hexadecimal literals [edit]

The standard recommends providing conversions to and from external hexadecimal-significand character sequences, based on C99'southward hexadecimal floating point literals. Such a literal consists of an optional sign (+ or -), the indicator "0x", a hexadecimal number with or without a period, an exponent indicator "p", and a decimal exponent with optional sign. The syntax is not case-sensitive.^[52] The decimal exponent scales by powers of ii, and so for example 0x0.1p-iv is 1/256.^[53]

Come across also [edit]

• bfloat16 floating-point format
• Binade
• Coprocessor
• C99 for code examples demonstrating access and utilise of IEEE 754 features.
• Floating-point arithmetic, for history, design rationale and case usage of IEEE 754 features.
• Fixed-signal arithmetic, for an alternative approach at ciphering with rational numbers (peculiarly beneficial when the exponent range is known, fixed, or bound at compile time).
• IBM System z9, the get-go CPU to implement IEEE 754-2008 decimal arithmetic (using hardware microcode).
• IBM z10, IBM z196, IBM zEC12, and IBM z13, CPUs that implement IEEE 754-2008 decimal arithmetics fully in hardware.
• ISO/IEC 10967, language-independent arithmetic (LIA).
• Minifloat, depression-precision binary floating-point formats following IEEE 754 principles.
• POWER6, POWER7, and POWER8 CPUs that implement IEEE 754-2008 decimal arithmetic fully in hardware.
• strictfp, a keyword in the Java programming linguistic communication that restricts arithmetics to IEEE 754 unmarried and double precision to ensure reproducibility across common hardware platforms.
• Table-maker'southward dilemma for more about the right rounding of functions.
• Standard Apple tree Numerics Environment
• Tapered floating indicate

Notes [edit]

1. ^ For example, if the base of operations is ten, the sign is 1 (indicating negative), the significand is 12345, and the exponent is −3, so the value of the number is (−ane)¹ × 12345 × 10⁻³ = −1 × 12345 × 0.001 = −12.345.
2. ^ Including the implicit bit (which always equals 1 for normal numbers, and 0 for subnormal numbers. This implicit fleck is not stored in memory), but not the sign bit.
3. ^ Reverse to decimal, in that location is no binary interchange format of 96-fleck length. Such a format is however immune every bit a not-interchange format, though.
4. ^ The standard recommends 0 for signaling NaNs, one for repose NaNs, so that a signaling NaNs can be quieted by changing only this bit to 1, while the reverse could yield the encoding of an infinity.
5. ^ No flag is raised in certain cases of underflow.
6. ^ As an implementation limit, correct rounding is only guaranteed for the number of decimal digits required plus three for the largest supported binary format. For example, if binary32 is the largest supported binary format, and then a conversion from a decimal external sequence with 12 decimal digits is guaranteed to exist correctly rounded when converted to binary32; but conversion of a sequence of thirteen decimal digits is non; however, the standard recommends that implementations impose no such limit.

References [edit]

1. ^ IEEE 754 2019
2. ^ "FW: ISO/IEC/IEEE 60559 (IEEE Std 754-2008)". grouper.ieee.org. Archived from the original on 2017-ten-27. Retrieved 2018-04-04 .
3. ^ "ISO/IEEE Partner Standards Development Organization (PSDO) Cooperation Agreement" (PDF). 2007-12-xix. Retrieved 2021-12-27 .
4. ^ "ISO/IEC/IEEE 60559:2011 — It — Microprocessor Systems — Floating-Point arithmetic". www.iso.org . Retrieved 2018-04-04 .
5. ^ ^{a b} Cowlishaw, Mike (2013-11-13). "IEEE 754-2008 errata". speleotrove.com . Retrieved 2020-01-24 .
6. ^ "Revising ANSI/IEEE Std 754-2008". ucbtest.org . Retrieved 2018-04-04 .
7. ^ "ISO/IEC 60559:2020 — Information technology — Microprocessor Systems — Floating-Bespeak arithmetic". www.iso.org . Retrieved 2020-10-25 .
8. ^ Riedy, E. Jason (2018-06-26), "Plans for IEEE Standard 754 – 2028" (PDF), 25th IEEE Symposium on Computer Arithmetic, Amherst, MA: IEEE {{citation}}: CS1 maint: date and twelvemonth (link)
9. ^ IEEE 754 2008, §ii.1.27.
10. ^ "SpiderMonkey Internals". developer.mozilla.org . Retrieved 2018-03-11 .
11. ^ Klemens, Ben (September 2014). 21st Century C: C Tips from the New School. O'Reilly Media, Incorporated. p. 160. ISBN9781491904442 . Retrieved 2018-03-11 .
12. ^ "zuiderkwast/nanbox: NaN-battle in C". GitHub . Retrieved 2018-03-xi .
13. ^ IEEE 754 2008, §3.6.
14. ^ Cowlishaw, Mike. "Decimal Arithmetic Encodings" (PDF). IBM. Retrieved 2015-08-06 .
15. ^ IEEE 754 2008, §3.7.
16. ^ IEEE 754 2008, §3.7 states: "Language standards should define mechanisms supporting extendable precision for each supported radix."
17. ^ IEEE 754 2008, §3.vii states: "Language standards or implementations should back up an extended precision format that extends the widest basic format that is supported in that radix."
18. ^ IEEE 754 2019, §2.1
19. ^ IEEE 754 2008, §5.3.one
20. ^ IEEE 754 2008, §5.iv.1
21. ^ IEEE 754 2008, §five.4.ii
22. ^ IEEE 754 2008, §5.4.three
23. ^ IEEE 754 2008, §5.3.ii
24. ^ IEEE 754 2008, §v.3.3
25. ^ IEEE 754 2008, §5.5.1
26. ^ IEEE 754 2008, §5.10
27. ^ IEEE 754 2008, §v.11
28. ^ IEEE 754 2008, §5.7.ii
29. ^ IEEE 754 2008, §five.7.4
30. ^ IEEE 754 2019, §v.11
31. ^ IEEE 754 2019, §v.10
32. ^ IEEE 754 2019, §v.x
33. ^ Herf, Michael (December 2001). "radix tricks". stereopsis : graphics.
34. ^ "9.four. decimal — Decimal stock-still point and floating indicate arithmetic — Python iii.vi.5 documentation". docs.python.org . Retrieved 2018-04-04 .
35. ^ "Decimal Arithmetic - Infrequent conditions". speleotrove.com . Retrieved 2018-04-04 .
36. ^ IEEE 754 2008, §7.2(h)
37. ^ IEEE 754 2019, §9.2
38. ^ IEEE 754 2008, Clause 9
39. ^ IEEE 754 2019, §9.two.
40. ^ "Re: Missing functions tanPi, asinPi and acosPi". grouper.ieee.org. Archived from the original on 2017-07-06. Retrieved 2018-04-04 .
41. ^ IEEE 754 2008, §nine.3.
42. ^ IEEE 754 2008, §9.4.
43. ^ IEEE 754 2019, §9.5
44. ^ Riedy, Jason; Demmel, James. "Augmented Arithmetic Operations Proposed for IEEE-754 2018" (PDF). 25th IEEE Symbosium on Calculator Arithmetic (ARITH 2018). pp. 49–56. Archived (PDF) from the original on 2019-07-23. Retrieved 2019-07-23 .
45. ^ "754 Revision targeted for 2019". 754r.ucbtest.org . Retrieved 2019-07-23 .
46. ^ IEEE 754 2019, §ix.6.
47. ^ Chen, David. "The Removal of MinNum and MaxNum Operations from IEEE 754-2019" (PDF). grouper.ieee.org . Retrieved 2020-02-05 .
48. ^ IEEE 754 2008, §5.12.
49. ^ IEEE 754 2008, §5.12.2.
50. ^ Gay, David Thou. (1990-xi-30). "Correctly rounded binary-decimal and decimal-binary conversions". Numerical Analysis Manuscript. Murry Hill, NJ, USA: AT&T Laboratories. 90-10.
51. ^ Paxson, Vern; Kahan, William (1991-05-22). "A Program for Testing IEEE Decimal–Binary Conversion". Manuscript. CiteSeerX10.1.1.144.5889.
52. ^ IEEE 754 2008, §5.12.three
53. ^ "six.ix.iii. Hexadecimal floating indicate literals — Glasgow Haskell Compiler nine.iii.20220129 User's Guide". ghc.gitlab.haskell.org . Retrieved 2022-01-29 .

Standards [edit]

• "IEEE Standard for Binary Floating-Point Arithmetic". ANSI/IEEE Std 754-1985. 1985-x-12. doi:10.1109/IEEESTD.1985.82928.
• IEEE Computer Society (2008-08-29). IEEE Standard for Floating-Point Arithmetic. IEEE STD 754-2008. IEEE. pp. i–seventy. doi:10.1109/IEEESTD.2008.4610935. ISBN978-0-7381-5753-five. IEEE Std 754-2008.
• IEEE Computer Society (2019-07-22). IEEE Standard for Floating-Betoken Arithmetic. IEEE STD 754-2019. IEEE. pp. i–84. doi:x.1109/IEEESTD.2019.8766229. ISBN978-1-5044-5924-ii. IEEE Std 754-2019.
• ISO/IEC/IEEE 60559:2011 — Information technology — Microprocessor Systems — Floating-Point arithmetic. Iso.org. June 2011. pp. 1–58.
• ISO/IEC 60559:2020 — Information technology — Microprocessor Systems — Floating-Point arithmetic. Iso.org. May 2020. pp. 1–74.

Secondary references [edit]

• Decimal floating-point arithmetic, FAQs, bibliography, and links
• Comparing binary floats
• IEEE 754 Reference Fabric
• IEEE 854-1987 – History and minutes
• Supplementary readings for IEEE 754. Includes historical perspectives.

Further reading [edit]

• Goldberg, David (March 1991). "What Every Calculator Scientist Should Know About Floating-Point Arithmetic". ACM Computing Surveys. 23 (1): five–48. doi:10.1145/103162.103163. S2CID 222008826. Retrieved 2019-03-08 .
• Hecker, Chris (February 1996). "Let'southward Become To The (Floating) Bespeak" (PDF). Game Programmer Mag: 19–24. ISSN 1073-922X.
• Severance, Charles (March 1998). "IEEE 754: An Interview with William Kahan" (PDF). IEEE Reckoner. 31 (3): 114–115. doi:10.1109/MC.1998.660194. S2CID 33291145. Retrieved 2019-03-08 .
• Cowlishaw, Mike (June 2003). "Decimal Floating-Point: Algorism for Computers". 16th IEEE Symposium on Computer Arithmetic, 2003. Proceedings (PDF). Proceedings 16th IEEE Symposium on Computer Arithmetic. Los Alamitos, Calif.: IEEE Computer Society. pp. 104–111. doi:x.1109/ARITH.2003.1207666. ISBN978-0-7695-1894-vii. S2CID 18713046. Retrieved 2014-11-14 . . (Notation: Algorism is non a misspelling of the title; see besides algorism.)
• Monniaux, David (May 2008). "The pitfalls of verifying floating-point computations". ACM Transactions on Programming Languages and Systems. 30 (three): i–41. arXiv:cs/0701192. doi:10.1145/1353445.1353446. ISSN 0164-0925. S2CID 218578808. : A compendium of not-intuitive behaviours of floating-bespeak on popular architectures, with implications for program verification and testing.
• Muller, Jean-Michel; Brunie, Nicolas; de Dinechin, Florent; Jeannerod, Claude-Pierre; Joldes, Mioara; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Torres, Serge (2018) [2010]. Handbook of Floating-Betoken Arithmetic (two ed.). Birkhäuser. doi:10.1007/978-3-319-76526-6. ISBN978-three-319-76525-ix.
• Overton, Michael L. (2001). Written at Courant Institute of Mathematical Sciences, New York University, New York, Usa. Numerical Computing with IEEE Floating Point Arithmetic (1 ed.). Philadelphia, United states: SIAM. doi:10.1137/i.9780898718072. ISBN978-0-89871-482-1. 978-0-89871-571-2, 0-89871-571-7.
• Cleve Moler on Floating Point numbers
• Beebe, Nelson H. F. (2017-08-22). The Mathematical-Function Computation Handbook - Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake Urban center, UT, Us: Springer International Publishing AG. doi:10.1007/978-iii-319-64110-two. ISBN978-3-319-64109-vi. LCCN 2017947446. S2CID 30244721.
• Hough, David G. (December 2019). "The IEEE Standard 754: I for the History Books". Computer. IEEE. 52 (12): 109–112. doi:10.1109/MC.2019.2926614. S2CID 208281213.

External links [edit]

Wikimedia Commons has media related to IEEE 754.

• Kahan on creating IEEE Standard Floating Point. Turing Awardee Clips. 2020-11-16. Archived from the original on 2021-eleven-08.
• Online IEEE 754 binary calculators

williamsdemuchys.blogspot.com

Source: https://en.wikipedia.org/wiki/IEEE_754

Share this post